オバマ大統領が勝利しましたね。これでしばらくはFRB頼みになってしまいます。前回の続き、ポートフォリオの最適化について今日はお話ししたいと思います。
まずは、前回もお話ししたようにパフォーマンスが優れているものを寄せ集めれば良い。というわけではありませんね。分散させてポートフォリヲを構成する際に気をつけるべきことは選定する各資産クラスがどのような相互作用があるかどうかが重要なポイントとなります。
この考え方は、1990年「資産運用の安全性を高めるための一般理論形成」にてノーベル経済学賞を受賞したアメリカの経済学者ハリー・マーコウィッツの提案です。
・投資とはリスクと期待リターンのトレードオフである。通常、資産は高い期待リターンであればリスクも高くなる。
・モダンポートフォリヲ理論の基本コンセプトは、ポートフォリオの中にある資産を孤立させて選定するのではなく、それぞれのメリットを
活かすように選定する。重要なのは、それぞれの資産価格が変動するときに、その他の資産が相関してどのような値動きをするかである。
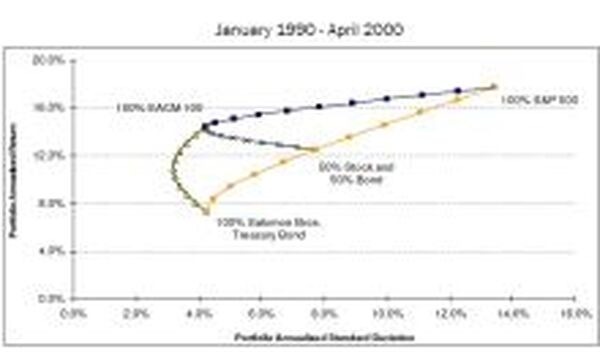
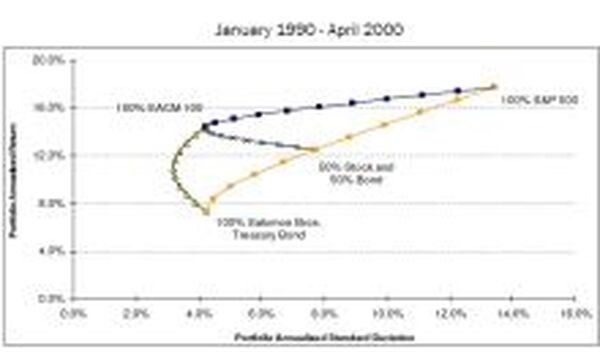
この表をご覧下さい。
これはポートフォリオの資産クラスの割合で標準偏差とリターンがどのように変化するかをグラフにしたものです。オレンジ色のグラフに注目してください。右に行けば行くほど株式の割合が高くなり、左に行けば行くほど債券の割合が高くなっています。
株式の比率が高くなればリターンも高くなりますが、その分標準偏差も上がりリスクも高くなります。上の紺色の線はヘッジファンドを混ぜた場合です。左に行けばヘッジファンドの割合が高くなり、右に行くほど株式の割合が高くなります。ヘッジファンドを100%保有したとしても、標準偏差は低くなっていますが、高いリターンを維持していますね。
’90-’00の結果なので、ヘッジファンド全盛期だから・・・という気もいたしますが、資料として参考にしてみてください。ポートフォリオを構成する際によく利用する指標を相関係数といいます。
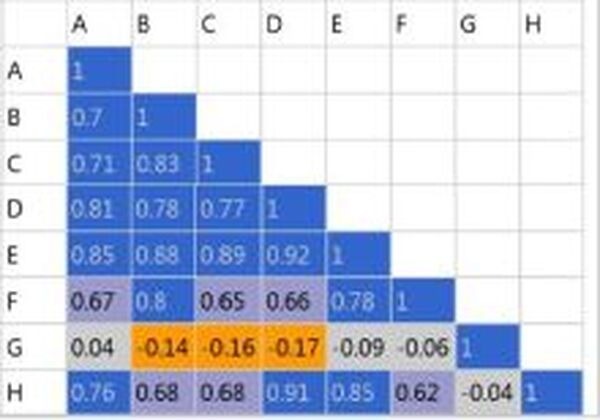
-1から1の間で二つの資産クラスの相関度を表してくれます。
-1に近づけば近づくほど反相関、つまり全く逆の動きをみせ、1に近づくほど同じ動きをみせるという意味です。
下の表は実際に組んだポートフォリオの相関係数の表です。
このように、反相関しているものでヘッジしつつ全体的に相関して増やしていく構成が理想ですかね。今週はここまで!